Get the optimal forward difference interval by Gill83 method
nlmixrGill83(
what,
args,
envir = parent.frame(),
which,
gillRtol = sqrt(.Machine$double.eps),
gillK = 10L,
gillStep = 2,
gillFtol = 0
)Arguments
- what
either a function or a non-empty character string naming the function to be called.
- args
a list of arguments to the function call. The
namesattribute ofargsgives the argument names.- envir
an environment within which to evaluate the call. This will be most useful if
whatis a character string and the arguments are symbols or quoted expressions.- which
Which parameters to calculate the forward difference and optimal forward difference interval
- gillRtol
The relative tolerance used for Gill 1983 determination of optimal step size.
- gillK
The total number of possible steps to determine the optimal forward/central difference step size per parameter (by the Gill 1983 method). If 0, no optimal step size is determined. Otherwise this is the optimal step size determined.
- gillStep
When looking for the optimal forward difference step size, this is This is the step size to increase the initial estimate by. So each iteration the new step size = (prior step size)*gillStep
- gillFtol
The gillFtol is the gradient error tolerance that is acceptable before issuing a warning/error about the gradient estimates.
Value
A data frame with the following columns:
infoGradient evaluation/forward difference information
hfForward difference final estimate
dfDerivative estimate
df22nd Derivative Estimate
errError of the final estimate derivative
aEpsAbsolute difference for forward numerical differences
rEpsRelative Difference for backward numerical differences
aEpsCAbsolute difference for central numerical differences
rEpsCRelative difference for central numerical differences
The info returns one of the following:
Not AssessedGradient wasn't assessed
GoodSuccess in Estimating optimal forward difference interval
High Grad ErrorLarge error; Derivative estimate error
fTolor more of the derivativeConstant GradFunction constant or nearly constant for this parameter
Odd/Linear GradFunction odd or nearly linear, df = K, df2 ~ 0
Grad changes quicklydf2 increases rapidly as h decreases
Examples
## These are taken from the numDeriv::grad examples to show how
## simple gradients are assessed with nlmixrGill83
nlmixrGill83(sin, pi)
#> Gill83 Derivative/Forward Difference
#> (rtol=1.49011611938477e-08; K=10, step=2, ftol=0)
#>
#> info hf hphi df df2 err aEps
#> 1 Odd/Linear Grad 2.237911e-11 1.118956e-11 -1 0 1.630865e-13 5.403504e-12
#> rEps aEpsC rEpsC f
#> 1 5.403504e-12 5.403504e-12 5.403504e-12 1.224647e-16
nlmixrGill83(sin, (0:10)*2*pi/10)
#> Gill83 Derivative/Forward Difference
#> (rtol=1.49011611938477e-08; K=10, step=2, ftol=0)
#>
#> info hf hphi df df2
#> 1 Grad changes quickly 1.045337e-07 5.226686e-08 1.0000000 8.796093e+12
#> 2 Grad changes quickly 1.702142e-07 8.510710e-08 0.8090170 4.254583e+19
#> 3 Grad changes quickly 2.358947e-07 1.179473e-07 0.3090168 3.584264e+19
#> 4 Grad changes quickly 3.015752e-07 1.507876e-07 -0.3090171 2.193033e+19
#> 5 Grad changes quickly 3.672556e-07 1.836278e-07 -0.8090173 9.139274e+18
#> 6 Grad changes quickly 4.329361e-07 2.164681e-07 -1.0000004 7.692125e+11
#> 7 Grad changes quickly 4.986166e-07 2.493083e-07 -0.8090174 -4.958098e+18
#> 8 Grad changes quickly 5.642971e-07 2.821485e-07 -0.3090169 -6.263551e+18
#> 9 Grad changes quickly 6.299776e-07 3.149888e-07 0.3090172 -5.025578e+18
#> 10 Grad changes quickly 6.956580e-07 3.478290e-07 0.8090169 -2.547164e+18
#> 11 Good 2.441411e-04 7.796106e-04 1.0000000 4.583226e-08
#> err aEps rEps aEpsC rEpsC
#> 1 4.597442e+05 1.045337e-07 1.045337e-07 1.045337e-07 1.045337e-07
#> 2 3.620952e+12 1.045337e-07 1.045337e-07 1.045337e-07 1.045337e-07
#> 3 4.227544e+12 1.045337e-07 1.045337e-07 1.045337e-07 1.045337e-07
#> 4 3.306821e+12 1.045337e-07 1.045337e-07 1.045337e-07 1.045337e-07
#> 5 1.678225e+12 1.045337e-07 1.045337e-07 1.045337e-07 1.045337e-07
#> 6 1.665099e+05 1.045337e-07 1.045337e-07 1.045337e-07 1.045337e-07
#> 7 1.236095e+12 1.045337e-07 1.045337e-07 1.045337e-07 1.045337e-07
#> 8 1.767252e+12 1.045337e-07 1.045337e-07 1.045337e-07 1.045337e-07
#> 9 1.583001e+12 1.045337e-07 1.045337e-07 1.045337e-07 1.045337e-07
#> 10 8.859777e+11 1.045337e-07 1.045337e-07 1.045337e-07 1.045337e-07
#> 11 1.118954e-11 3.352119e-05 3.352119e-05 3.352119e-05 3.352119e-05
#> f
#> 1 -4.583242e-08
#> 2 -4.583242e-08
#> 3 -4.583242e-08
#> 4 -4.583242e-08
#> 5 -4.583242e-08
#> 6 -4.583242e-08
#> 7 -4.583242e-08
#> 8 -4.583242e-08
#> 9 -4.583242e-08
#> 10 -4.583242e-08
#> 11 -4.583242e-08
func0 <- function(x){ sum(sin(x)) }
nlmixrGill83(func0 , (0:10)*2*pi/10)
#> Gill83 Derivative/Forward Difference
#> (rtol=1.49011611938477e-08; K=10, step=2, ftol=0)
#>
#> info hf hphi df df2
#> 1 Grad changes quickly 7.391651e-08 3.695825e-08 1.0000000 1.203250e+17
#> 2 Grad changes quickly 1.203596e-07 6.017981e-08 0.8090168 4.538135e+16
#> 3 Grad changes quickly 1.668027e-07 8.340136e-08 0.3090166 2.362831e+16
#> 4 Grad changes quickly 2.132458e-07 1.066229e-07 -0.3090170 1.445699e+16
#> 5 Grad changes quickly 2.596889e-07 1.298445e-07 -0.8090170 9.748364e+15
#> 6 Odd/Linear Grad 3.061321e-07 1.530660e-07 -1.0000000 0.000000e+00
#> 7 High Grad Error 4.821089e-08 3.525752e-07 -0.8090170 5.876689e-01
#> 8 High Grad Error 3.788199e-08 3.990183e-07 -0.3090170 9.518254e-01
#> 9 Good 3.789588e-08 4.454614e-07 0.3090170 9.511281e-01
#> 10 Good 4.818847e-08 4.919045e-07 0.8090170 5.882158e-01
#> 11 Good 1.726341e-04 5.512680e-04 1.0000000 4.583208e-08
#> err aEps rEps aEpsC rEpsC
#> 1 4.447003e+09 7.391651e-08 7.391651e-08 7.391651e-08 7.391651e-08
#> 2 2.731041e+09 7.391651e-08 7.391651e-08 7.391651e-08 7.391651e-08
#> 3 1.970634e+09 7.391651e-08 7.391651e-08 7.391651e-08 7.391651e-08
#> 4 1.541446e+09 7.391651e-08 7.391651e-08 7.391651e-08 7.391651e-08
#> 5 1.265771e+09 7.391651e-08 7.391651e-08 7.391651e-08 7.391651e-08
#> 6 2.230920e-09 7.392210e-08 7.392210e-08 7.392210e-08 7.392210e-08
#> 7 2.833204e-08 1.010729e-08 1.010729e-08 1.010729e-08 1.010729e-08
#> 8 3.605704e-08 7.017484e-09 7.017484e-09 7.017484e-09 7.017484e-09
#> 9 3.604383e-08 6.288156e-09 6.288156e-09 6.288156e-09 6.288156e-09
#> 10 2.834522e-08 7.241087e-09 7.241087e-09 7.241087e-09 7.241087e-09
#> 11 7.912182e-12 2.370311e-05 2.370311e-05 2.370311e-05 2.370311e-05
#> f
#> 1 -2.291621e-08
#> 2 -2.291621e-08
#> 3 -2.291621e-08
#> 4 -2.291621e-08
#> 5 -2.291621e-08
#> 6 -2.291621e-08
#> 7 -2.291621e-08
#> 8 -2.291621e-08
#> 9 -2.291621e-08
#> 10 -2.291621e-08
#> 11 -2.291621e-08
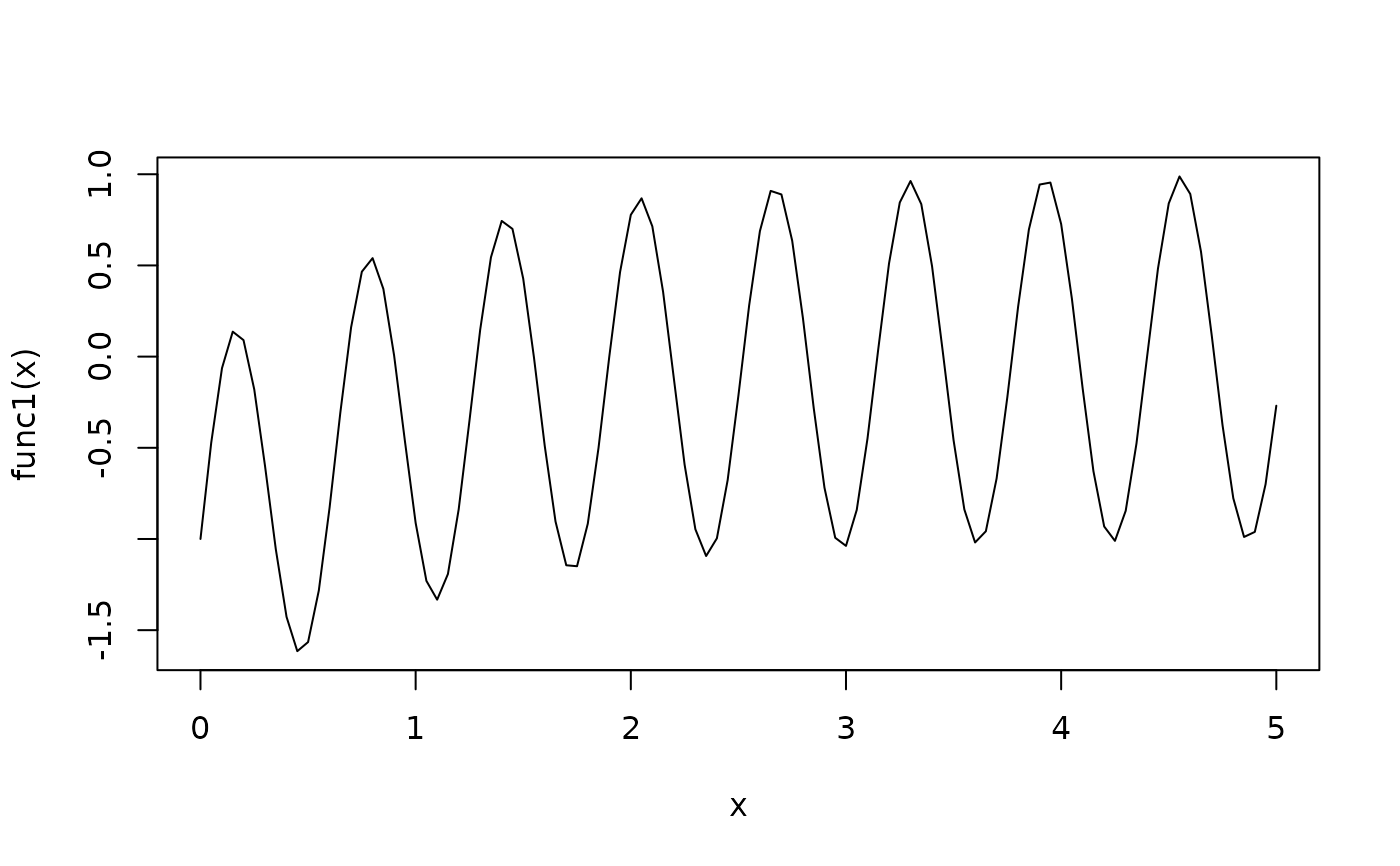
func1 <- function(x){ sin(10*x) - exp(-x) }
curve(func1,from=0,to=5)
x <- 2.04
numd1 <- nlmixrGill83(func1, x)
exact <- 10*cos(10*x) + exp(-x)
c(numd1$df, exact, (numd1$df - exact)/exact)
#> [1] 0.332398077 0.333537144 -0.003415112
x <- c(1:10)
numd1 <- nlmixrGill83(func1, x)
exact <- 10*cos(10*x) + exp(-x)
cbind(numd1=numd1$df, exact, err=(numd1$df - exact)/exact)
#> numd1 exact err
#> [1,] -8.022836 -8.022836 -1.369260e-11
#> [2,] 4.216156 4.216156 -2.839580e-11
#> [3,] 1.592302 1.592302 -1.150871e-11
#> [4,] -6.651065 -6.651065 -4.125002e-11
#> [5,] 9.656398 9.656398 -5.172856e-11
#> [6,] -9.521651 -9.521651 2.985064e-10
#> [7,] 6.334104 6.334104 -8.697948e-11
#> [8,] -1.103537 -1.103537 -9.731425e-11
#> [9,] -4.480613 -4.480613 -1.320695e-10
#> [10,] 8.623852 8.623234 7.167430e-05
sc2.f <- function(x){
n <- length(x)
sum((1:n) * (exp(x) - x)) / n
}
sc2.g <- function(x){
n <- length(x)
(1:n) * (exp(x) - 1) / n
}
x0 <- rnorm(100)
exact <- sc2.g(x0)
g <- nlmixrGill83(sc2.f, x0)
max(abs(exact - g$df)/(1 + abs(exact)))
#> [1] 0.001078841